기수 정렬(Radix Sort)에 대해 알아보자

이번 포스팅에서는 기수 정렬에 대해 알아보도록 하겠다. 기수 정렬은 시간복잡도가 가장 빠른 정렬방법으로 O(kn)의 시간복잡도를 가진다. 여기서 k는 정렬하고자 하는 숫자의 최대 자릿수이다. 만약 숫자의 범위가 999까지 라면 k=3인 것이다. 보통 시간복잡도를 쓸 때는 상수는 무시하는 것이 관례이다. n이 커질수록 상수가 의미가 없어지기 때문이다. 그런데 기수 정렬은 왜 상수를 표시해 놓았을까? 그것은 기수정렬에서는 자릿수가 가장 큰 변수 중 하나이기 때문이다. 만약 1~9까지의 수 10개와 1X10^99이라는 숫자가 하나 있다고 해 보자. 이 숫자들에 기수 정렬을 실시한다면 시간복잡도는 100이다. 저 큰 숫자만 없다면 시간복잡도는 1이다. 즉 자릿수에 따라 시간복잡도가 매우 유동적이므로 저렇게 표시한 것이다. 그러면 기수 정렬을 하는 방법을 알아보자. 설명에서는 999까지의 자연수로만 설명하겠다.

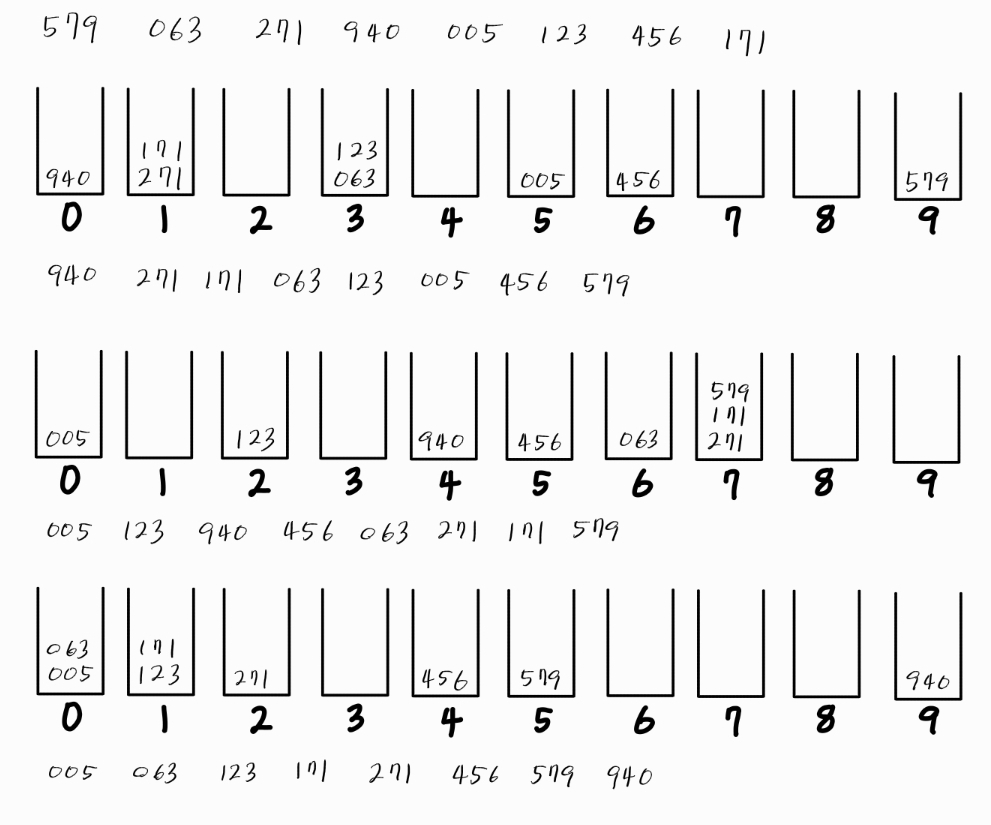
기수 정렬은 큐를 이용해 숫자를 분류한다. 그림이 스택같지만 무시하자... 먼저 모든 숫자를 각 자릿수별로 끊어서 읽거나, 저장해놔야 한다. 또한 최대 자릿수보다 모자라는 자릿수를 가진 숫자들은 앞에 0을 붙여 모두 최대 자릿수로 만들어주어야 한다. 한자리 숫자는 005처럼 만들어준 것을 볼 수 있다. 그리고 큐를 10개 선언하는데 이 큐들은 0~9까지의 숫자를 나타낼 것이다. 숫자를 큐에 넣을 때 제일 끝쪽인 일의 자리부터 자신과 똑같은 큐에 넣는다. 만약 579라면 9를 가리키는 큐에, 940이라면 0을 가리키는 큐에 넣는다. 숫자를 전부 넣으면 일의 자리가 같은 것들만 큐에 들어있을 것이다. 그러면 0번 큐부터 차례대로 숫자를 빼 앞에서부터 다시 배열한다. 즉, 1의 자리가 0인 숫자가 맨 앞으로 오게 배열한다. 그림에서 940이 제일 앞에 있는 것을 볼 수 있다. 그리고 이제 십의 자리로 이것을 반복한다. 숫자를 넣을 때는 앞에서부터(일의 자리가 0인 것들부터) 넣어야 한다. 그리고 다 넣으면 다시 빼고, 다시 백의 자리를 찾아 넣고... 이것을 모든 자릿수에 대해서 반복한다. 마지막으로 큐에서 빼면 정렬이 끝이다.

처음에 기수 정렬을 공부했을 때 잘 이해가 가지 않았다. 어떻게 숫자를 큐에 넣었다 빼기만 했는데 정렬이 끝나있는가? 이것은 큐가 선입선출 구조를 가지기 때문이다. 마지막 큐의 입출력에서 큐의 값이 0인 것부터 빼기 시작하는데 이것은 005와 같이 앞에 0을 붙여준 숫자들일 것이다. 즉 작은 숫자들이다. 그리고 1은 100번대 숫자가 나올것이고 2는 200번대가 나온다. 십의 자리로 거슬러 올라가면 십의 자리가 작은 것부터 나왔을 것이다. 일의 자리도 마찬가지 이므로 처음부터 차근차근 정렬을 했다고 할 수 있다. 직접 구현을 해 보면 이해가 더 잘될 것이다.

기수정렬을 구현할 때 큐를 이용하는것이 정석적인 방법이지만 더 빠른 방법도 있다. 나도 책을 보고 알았는데 구간 합을 이용하여 숫자들의 개수를 카운팅 하는 방법이다. 숫자를 전부 정수 배열에 담고 10개의 큐 대신 크기 10의 정수배열을 선언한다. 그리고 위의 그림처럼 숫자를 담는 것이 아니라 숫자의 개수를 누적 합으로 저장한다. 위의 예제에서 보면 0번 칸은 2개, 1번 칸은 2+2=4개, 2번 칸은 2+2+1=5개... 이렇게 숫자의 개수를 저장하는 것이 키 포인트이다. 숫자를 판별할 때는 최초 자릿수를 1로 설정하고 나머지 연산자 %를 사용한다. (456/1)%10=6이고 (456/10)%10=45%10=5인 것처럼 자릿수를 증가시키며 나누면 정수 연산이기 때문에 나머지를 버리게 되고 %로 끝자리 숫자를 알 수 있다. 이렇게 알게 된 끝자리 숫자로 10개의 배열에 ++연산을 해준다. 10개 배열[끝자리 숫자]++; 이렇게 말이다. 모든 수를 넣으면 합 배열로 만들어주고 숫자를 담은 배열에서 뒤에서부터 각 숫자를 다시 검사하여 새로 정렬하면 된다. 사실 말로 쓰니 나도 잘 모르겠다... 코드를 보자.

import java.io.*;
import java.util.*;

public class Main {
    static int N;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;
        N = Integer.parseInt(br.readLine());
        int[] array = new int[N];
        for(int i=0;i<N;i++){
            array[i] = Integer.parseInt(br.readLine());
        }
        radixSort(array, 5);
        for(int i=0;i<N;i++){
            bw.write(array[i]+"\n");
        }
        bw.flush();
        bw.close();
    }
    static void radixSort(int[] array, int num){
        int[] temp = new int[N];
        int cnt = 1;
        int number = 1;
        while(cnt <= num){
            int[] que = new int[10];
            for(int i=0;i<N;i++){
                que[array[i]/number%10]++;
            }
            for(int i=1;i<10;i++){
                que[i] += que[i-1];
            }
            for(int i=N-1;i>=0;i--){
                temp[que[array[i]/number%10]-1] = array[i];
                que[array[i]/number%10]--;
            }
            for(int i=0;i<N;i++){
                array[i] = temp[i];
            }
            number *= 10;
            cnt++;
        }
    }
}

가장 햇갈릴만한 부분은 왜 뒤에서부터 검사해서 숫자를 넣어주냐는 것일 것이다. 나도 처음에 코드를 작성할 때는 앞에서부터 반복문을 돌렸다가 정렬이 이상하게 되는 현상을 보았다. 이것은 같은 자릿수에 같은 숫자가 있더라도 다른 자릿수의 크기비교가 이미 되어있기 때문이다. 예를 들어 1~999 범위의 10개의 수가 있는데 거기에 100 이하의 수가 5, 15, 40, 60이 있다고 해 보자. 100의 자리를 비교할 순서일 때는 이미 10의 자리정렬이 끝났으므로 저 순서대로 배열에 존재할 것이다. 큐의 0의 인덱스는 백의자리가 0인 것이 4개이므로 4일 것이다. 이제 앞에서부터 정렬을 해보자. 5부터 정렬을 하게 되고 인덱스는 4이므로 배열의 3위치에 들어간다. 이상하지 않은가? 5가 전체에서 가장 작은 수 이므로 가장 첫 번째 배열에 들어가야 하지 않는가? 이전단계에서 이미 십의 자리가 정렬이 끝나 앞에는 작은 숫자부터 있다. 그런데 앞에서부터 정렬을 시작하고 배열의 인덱스는 끝 부분을 가리키고 있으므로 오류가 나는 것이다. 정확히 말하자면 10개의 배열에 저장되는 숫자가 해당 숫자들이 끝나는 지점의 인덱스이므로 큰 수부터 넣어야 하고 따라서 뒤에서부터 검사해야 하는 것이다.

 

관련 백준 문제로는 10989번이 있다.

https://www.acmicpc.net/problem/10989

10989번: 수 정렬하기 3

여기서는 기수 정렬을 큐를 이용해 풀면 메모리 초과가 난다...따라서 배열로 누적합을 이용하여 풀어야 한다.

이것으로 가장 많이 사용되는 배열의 종류는 전부 다루었다. 셸 소트, 힙 정렬 등의 방법이 더 있긴 하지만 나중에 시간이 되면 다루어보겠다. 다음 포스팅부터는 탐색방법에 대해 알아보갰다.